문제

https://www.acmicpc.net/problem/1740

풀이 과정

이 문제를 풀기전 비트 마스킹이라는 개념을 제대로 알지 못한 상태로 접근했다. 처음에는 수학적으로 접근했었다.

\(3^0 = 1\)\(3^1 = 3\)\(3^2=9\)\(3^3=27\) \(...\)

3의 거듭제곱은 위와같이 줄줄이 이어진다. 여기서 거듭제곱 합의 조합 을 만들어야되는데 합을 늘어놓았을때 각 합들의 값이 서로 겹치면 안되고 작은수에서 큰수 순서대로 배열되어야한다.

나는 여기서 아래와 같은 방법으로 수의 합을 만들었다.

1. 거듭제곱 수 중에서 하나를 임의로 선택한다.
2. 선택된 수보다 작은 수(거듭제곱 수 중)들로 만들수 있는 조합들을 모두 나열한다.

이렇게 합들을 구해서 나열하면 이런씩으로 정리할 수 있다. |임의 선택 수 | 합 경우의 수 | |–|–| |\(3^0\) | 1 | | \(3^1\) | 3 4 | | \(3^2\) | 9 10 13 12 | | \(3^3\) | 27 30 37 36 31 39 40 28 | |\(...\)|\(...\)| 이렇게 줄기와 잎 그림 스럽게 정리 할 수 있다. 이 그림을 보면 알 수 있듯이 합들이 서로 겹치지 않고 각 임의 선택 수들에 있는 합 경우의 수가 위, 아래의 값들 사이에 모두 존재하는 것을 확인할 수 있다.

여기서 고등학교 확률과 통계에서 배운 조합(Combination)을 활용할 수 있다.

조합(Combination)

\[_nC_r = \frac{n!}{r!(n-r)!}\]

이 공식을 활용하여 각 임의의 선택수에서 나올 수 있는 합의 경우의 수를 구하면 다음과 같다. |임의 선택 수 | 조합 수 | |–|–| |\(3^0\) | \(_0C_0\) | | \(3^1\) | \(_1C_0 + _1C_1\) | | \(3^2\) | \(_2C_0 + _2C_1 + _2C_2\) | | \(3^3\) | \(_3C_0 + _3C_1 + _3C_2 + _3C_3\) | |\(...\)|\(...\)|

사용자로 부터 N번째로 작은 수를 구해달라는 요청이 왔을때 임의 선택 수 의 조합수를 위에서부터 차례대로 N에서 뺄셈 함으로써 더이상 뺄셈이 안될때까지(이 이상 빼면 N<0 이 되는 경우) 진행한다음 뺄셈이 중단된 임의의 선택수의 경우의 수 부터 합을 검색하면 생으로 찾는것보다 연산 시간을 단축 시킬 수 있다.

예를 들어 N=14일때

\[14 - (_0C_0) - (_1C_0 + _1C_1) - (_2C_0 + _2C_1 + _2C_2) = 14 - 1 - 2 - 4 = 7\]

이 되고, 임의 선택 수가 $3^2$ 일때 나오는 경우의 수 중 7번째로 작은 수를 찾아서 출력하면 된다.

그런데 임의 선택수의 제곱수가 커질수록 이 조합수를 일일이 더하기에는 어려움이 생긴다. 이때 파스칼의 삼각형 을 활용할 수 있다.

파스칼의 삼각형(Pascal’s Triangle)

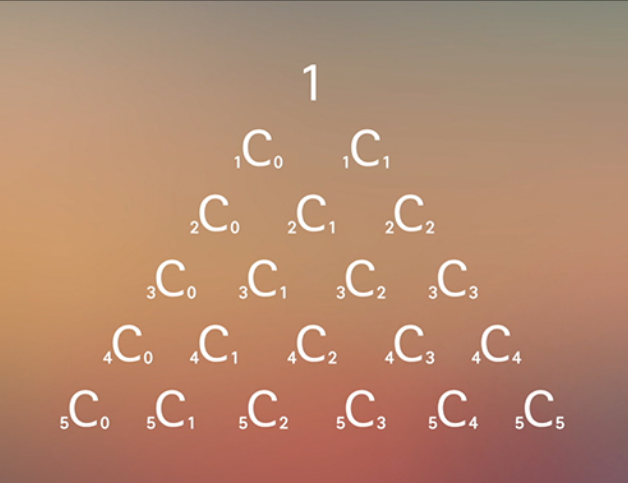출처 : (고교수학: 확률과 통계 │ EBSMath) (삼각형 최상단에 1은 $_0C_0$ 으로 취급)

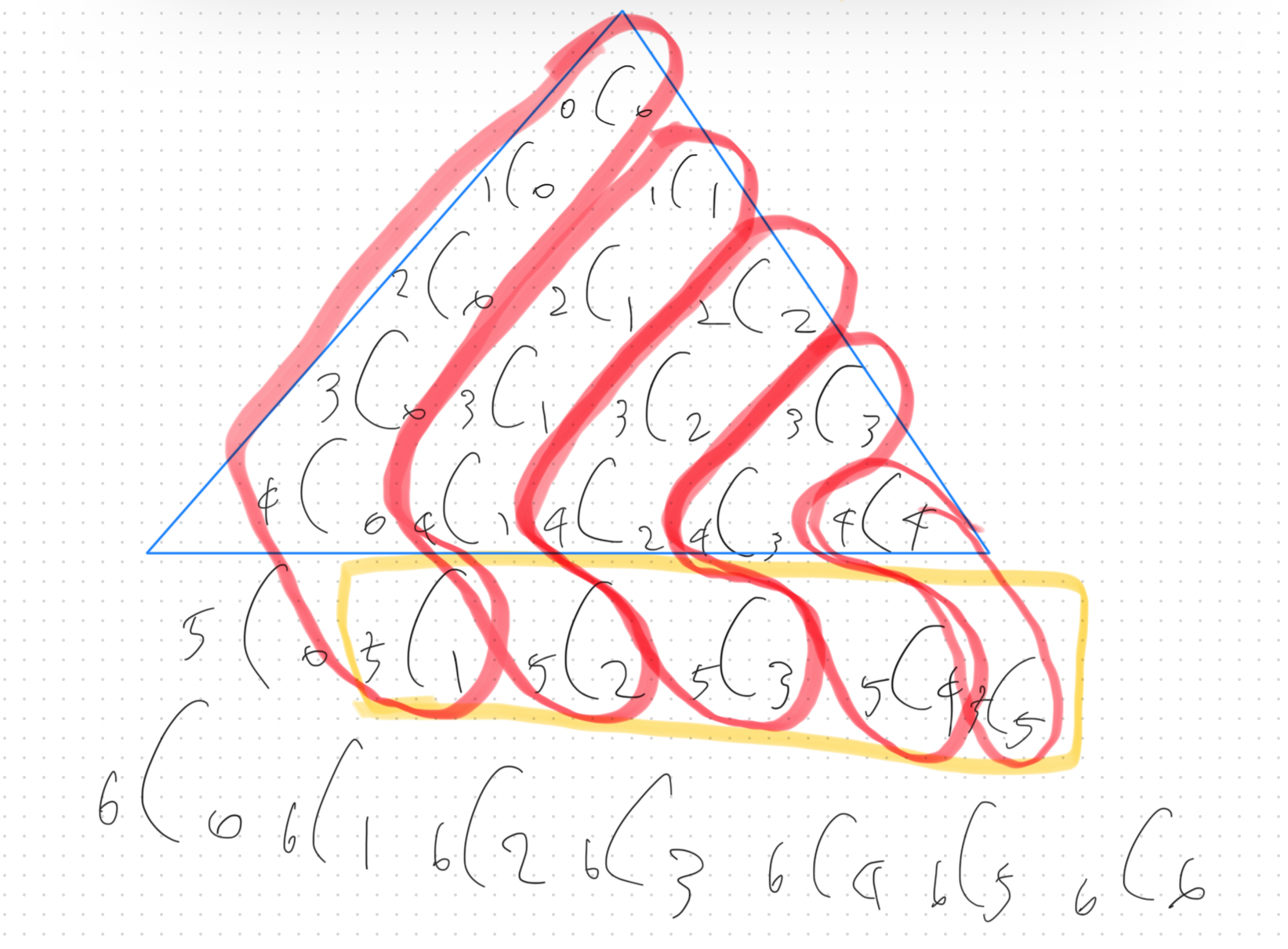
이 삼각형에서 활용할 수 있는 성질 중 하나가 소위 “하키스틱 패턴” 이다. 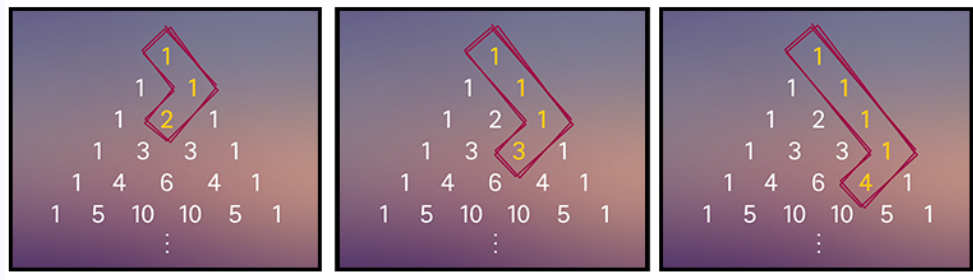출처 : (고교수학: 확률과 통계 │ EBSMath) 위 그림 처럼 양쪽 모서리에서 시작해서 하키스틱 모양으로 선을 이었을때 하키스틱의 일직선 부분을 모두 더했을때 하키스틱의 꺽인 끝부분의 값이 나오는 성질이다. 이를 위와같은 경우 이렇게 이용할 수 있다.

예를 들어 N=33일때 임의의 선택수가 $3^4$일때 조합수까지의 합이 필요한데 위 성질을 사용하면 아래처럼 단순화 시킬 수 있다. \(\sum_{n=0}^{4}{ _nC_0}={_5C_1}\newline \sum_{n=1}^{4}{ _nC_1}={_5C_2}\newline...\newline\sum_{n=4}^{4}{ _nC_4}={_5C_5} \newline\therefore\sum_{n=0}^{4}{\sum_{m=0}^{n}{ _nC_0}=\sum_{z=1}^{5}{_{5}C_z}}\)

따라서 이를 통해 아래 수식이 성립하는 것을 알 수 있다.

\(\sum_{n=0}^{k}{\sum_{m=0}^{n}{ _nC_0}=\sum_{z=1}^{k+1}{_{k+1}C_z}}\) 이렇게 수식을 단순화 한 후 최종적으로 이 조합들의 합을 구하는데는 이항정리를 같이 활용할 수 있다.

이항정리

\[(a+b)^k = \sum_{n=0}^k{a^n b^{k-n}{_kC_n}}\]

이 공식에서 a=1,b=1을 대입하면 아래와 같다.

\[2^k = \sum_{n=0}^k{_kC_n}\]

여기에서 양변에 1을 빼주면 이런 식을 얻을 수 있다.

\[2^k -1= \sum_{n=0}^k{_kC_n}-1=\sum_{n=1}^k{_kC_n}\]

이 공식을 활용하면 위에서 하키스틱 패턴을 이용해 정리한 식의 합을 구할 수 있다. 이를 이용해 위에서 구한 식을 풀면 다음과 같다. \(\sum_{n=1}^{5}{_{5}C_n} = 2^5-1=31\) 따라서 N에서 31을 빼면 2가 되므로 이를 통해 아래의 정보를 얻을 수 있다.

1. N=33일때 임의의 선택수가 $3^5$일때 조합 중에 존재한다.
2. 임의의 선택수가 $3^5$일때 나오는 값을 작은 순서 대로 나열 했을 때 2번째에 값이 존재한다.

그 다음 최종적으로 값을 알아내기 위해서는 해당 선택 수에서 조합될수 있는 수들을 어떤순서로 조합하여 더했을때 작은수에서 큰수 순서대로 나열할 수 있는지를 확인해야한다.

여러번의 경우를 확인해본결과 아래와 같은 순서대로 합을 나열하였을때 위 조건을 만족했다.

1. 임의의 수 혼자만 있을때 가장 작은수.
2. 임의의 수보다 작은수중에서 가장 작은 수를 임의로 또 선택 후 합 구하기
3. 그 다음으로 작은수를 임의로 선택후 그 수를 기준으로 또 작은수까지 함께 더하기.
4. 이를 반복. 말로 설명하니 어려우니 좀더 쉽게 비유를 해보려고 한다. 첫 임의의 수가 $3^5$일때 조합할 수 있는수는 아래와 같다.

| $3^4$ | $3^3$ | $3^2$ | $3^1$ | $3^0$ | | —– | —– | —– | —– | —– |

각 수를 켰다 껏다 할 수 있는 스위치로 상상해보자 | $3^4$ | $3^3$ |$3^2$ |$3^1$ |$3^0$ | |–|–|–|–|–| |OFF|OFF|OFF|OFF|OFF| 먼저 $3^0$을 켠다. | $3^4$ | $3^3$ |$3^2$ |$3^1$ |$3^0$ | |–|–|–|–|–| |OFF|OFF|OFF|OFF|ON| 이상태가 아무것도 안합친수 다음으로 작은수다. 그다음 $3^0$을 끄고 $3^1$을 켠다.

이게 그다음으로 작은수가 된다. 이상태로 $3^0$을 켠다. | $3^4$ | $3^3$ |$3^2$ |$3^1$ |$3^0$ | |–|–|–|–|–| |OFF|OFF|OFF|ON|ON| 이게 그 다음 작은수. 그다음 다끈다음 $3^2$를 켜면 그다음 작은수가 되고 이를 아래처럼 될때까지 반복하면 차례대로 작은수가 나열된다. | $3^4$ | $3^3$ |$3^2$ |$3^1$ |$3^0$ | |–|–|–|–|–| |ON|ON|ON|ON|ON| 이를 반복문으로 구현해서 최종적으로 작은수를 검색하여 출력하도록 하면 문제 해결…. 일줄 알았으나… … 시간 초과다. 생각보다 금방 해결될 줄 알았으나, 해결책이 떠오르기까지 거의 하루종일 걸렸다. 도저히 해결책이 떠오르지 않아 해당 문제의 알고리즘 분류를 확인했는데 비트마스킹 이라는 단어가 보였다.

용어 정의를 인터넷을 찾아보았다.

비트마스크(Bit Mask)

정수의 이진표현(2진수)를 자료구조로 활용하는 기법

이걸 확인하고 이 기법을 적용할 수 있는 부분이 있는지 확인하던 도중 위에서 스위치를 가지고 예시를 든 알고리즘이 눈에 들어왔다.

작은수를 순서대로 계산해서 나열하는 순서가 2진수값을 0에서부터 1씩 더했을때 나오는 자료구조와 유사한 것을 발견한것이다.

똑같이 for문을 활용하되 아래와 같이 알고리즘을 수정했다.

1. n=0 에서 1씩 증가
2. n을 2진수로 바꿔 문자열로 저장.
3. 다시 문자열의 길이만큼 반복문을 돌려서 숫자가 1인 인덱스의 값은 더하고 0이면 무시하도록함
4. 최종적으로 n번째 수에 도달하면 결과를 출력.

그러나 역시나 또 에러가 발생했다. (정신이 나갈것 같다….) 또 다른 부분에서 시간초과가 나는지 의미없는 디버깅만 도 계속하고 구글링을 하던 도중 비트 연산에 대한 글을 보게 되었다.

이글에서 어떤수에 또다른 수를 논리 연산자로 계산하면 2진수기준으로 각 자리가 논리연산자로 계산되면서 최종 결과를 내놓게 된다는 거였다. 예를들어 3과 11을 AND(&) 연산자로 연산한다고 하면 아래와 같이 연산이 된다는 것이다. | 3 | 11 |1 | |–|–|–| |1|1|1| |1|0|0| |0|1|0| |0|1|0| 즉 1이 된다.

이를 활용하여 이런 아이디어가 떠올랐다.

1. 어떤수가 되었든 그수와 1을 AND(&) 연산을 하게 되면 가장 작은 자릿수에 있는 2진수가 결과로 나오게 됨.
2. 비트를 우측으로 시프트하고 1번과정을 반복하면 모든 자리의 2진수를 확인할 수 있다.

특히나 비트연산작업의 시간 복잡도는 O(1)에 근접하기때문에 시간초과 문제를 해결하기에 완벽한 해결책이라고 생각했고 최종적으로 아래와 같이 코드를 작성하게 되었고. 드디어 문제를 푸는데 성공하였다.

import java.util.Scanner;
public class Main
{
	// 제곱 함수
    static long power(long x, long y){
        long result = 1;
        for(int i=0; i<y; i+=1) result *= x;
        return result;
    }
    // 조합수 합 계산 함수
    static long squareCombination(long n) {
        return power(2,n)-1;
    }
	public static void main(String[] args) {
		Scanner scan = new Scanner(System.in);
	    long n = Long.parseLong(scan.next());
	    long square,res=0,tmp;
	    // 조합 연산을 이용해 임의의 수 값 구하기, n 뺄셈
	    for(square = 0; squareCombination(square+1)<n; square += 1);
	    n -= squareCombination(square);
	    res += power(3,square);
	    tmp = n-1;
	    // 비트 연산을 통해 최종값 구하기
	    for(long i=0; tmp != 0; i+=1) {
	        res += (tmp&1) == 1 ? power(3,i):0;
	        tmp = tmp >> 1;
	    }
	    System.out.println(res);
	}
}

$※^1$ 위에서 언급 못했는데, 유저가 입력하는 N의 값의 예상 최대치가 $5\times10^{11}$여서 N을 포함한 큰수가 포함될것으로 예상되는 변수는 모두 int가 아닌 long으로 선언했다. | 타입 | 최대 값 | |–|–| | int | 2,147,483,647 | | long | 9,223,372,036,854,775,807 | $※^2$원래 자바에 기본 내장된 Math.pow()함수를 활용하려고 하였으나, 해당 함수는 부동 소수점 연산후 결과를 실수로 반환하므로 일부 부정확한 결과를 발생시킬 수 있어서 직접 자작하여 사용하였음.